Processamento Digital de Imagens

A figura a seguir dá uma visão geral da relação entre a área de processamento digital de imagens e outras disciplinas.

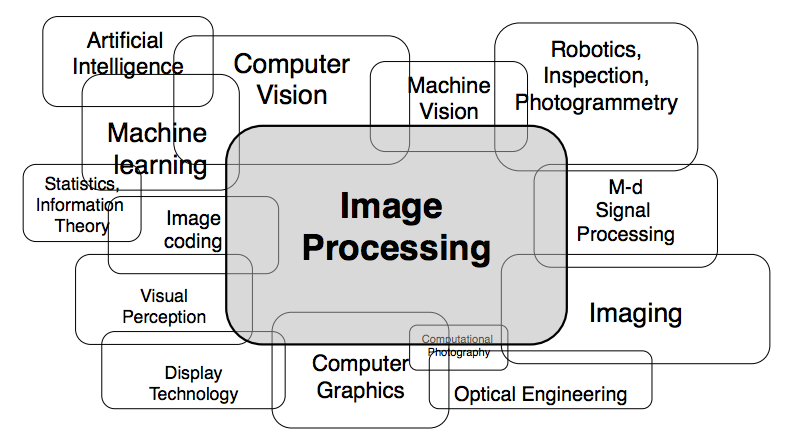
(BERND GIROD, G. W. Digital Image Processing. Stanford University (notas de aula))

Modelo matemático de formação de imagem

Uma imagem pode ser definida como uma função bidimensional $f(x,y)$ em que $x$ e $y$ são coordenadas espaciais (plano) e a amplitude de $f$ em qualquer par de coordenadas $(x,y)$ é chamada intensidade ou nível de cinza da imagem nesse ponto. Quando $x$, $y$ e os valores de intensidade de $f$ são quantidades finitas e discretas, chamamos de imagem digital.

A função $f(x,y)$ pode ser caracterizada por dois componentes:

1. iluminação: representada por $i(x,y)$, indica a quantidade de iluminação da fonte que incide na cena que está sendo vista; e
2. refletância: representada por $r(x,y)$, indica a quantidade de iluminação refletida pelos objetos na cena.

Ao combinar as duas funções temos:

$$f(x,y) = i(x,y) \times r(x,y)$$

onde:

• $0 \lt i(x,y) \lt \infty$
• $0 \lt r(x,y) \lt 1$

Os limites da refletância são chamados de:

• $0$: absorção total
• $1$: refletância total

Amostragem e quantização de imagens

A figura a seguir mostra uma imagem contínua $f$ que queremos converter em formato digital. Para isso, temos de fazer a amostragem da função em ambas as coordenadas e na amplitude. A digitalização dos valores de coordenada é chamada amostragem. A digitalização dos valores de amplitude é chamada de quantização.

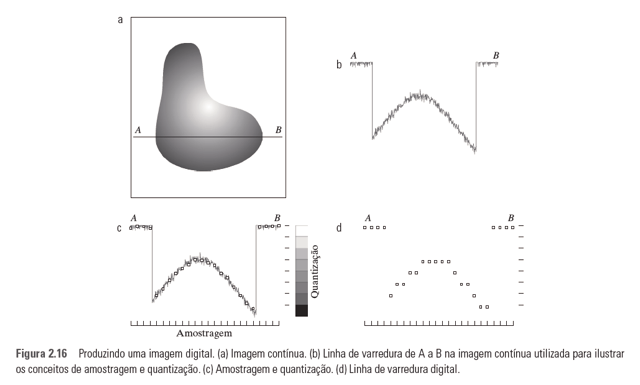
A figura a seguir ilustra o resultado do processo de amostragem e quantização.

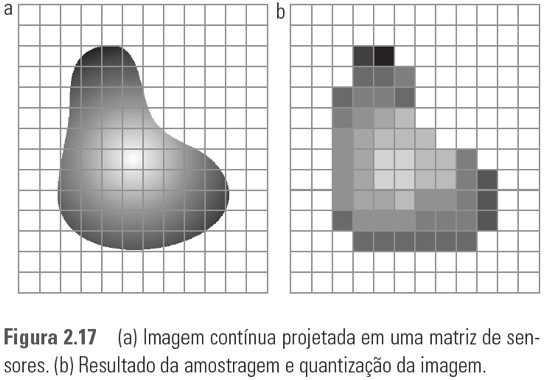
Representação do pixel (valores de intensidade)

A forma mais comum de representar $f$ é na forma de uma matriz $M \times N$ em que cada elemento $a_{i,j}$ está associado a um pixel na coordenada $(x,y)$. Nessa representação, $x = 0, 1, 2, ..., M - 1$ e $y = 0, 1, 2, ..., N - 1$.

Outra forma de representar $f$ é utilizando um vetor em que a relação entre o índice do vetor e o pixel da matriz é dada por:

$$i = x + M \times y$$

As posições $x$ e $y$ de um pixel para um índice $i$ do vetor podem ser obtidas por:

$$x = i \mbox{ mod } M \\ y = \frac{i}{M}$$

A imagem digital é composta por elementos chamados pixels, cada qual armazenando um valor de intensidade. O valor de intensidade é representado em um intervalo:

$$[0, 2^b - 1]$$

onde $b$ representa a quantidade de bits ou a profundidade de bits da imagem. Geralmente, este valor é limitado em 8 bits por banda do espectro de cor.

No caso de imagens monocromáticas, há apenas uma banda (por isso são geralmente chamadas imagens em tons de cinza).

No caso de imagens coloridas, pode haver mais de duas bandas. O sistema de cor RGB (do inglês Red, Green, Blue) representa três bandas baseadas nas cores primárias vermelho, verde e azul.

Padrões de representação da imagem em programação (e algoritmos)

Ao adotarmos a forma de representação da imagem por uma matriz $M \times N$ costumamos trabalhar com os índices $i$, para linhas, e $j$, para colunas. Assim, o algoritmo a seguir ilustra um percurso por todos os pixels da imagem:

para i de 0 até (M - 1) faça
    para j de 0 até (N - 1) faça
        I(i,j) representa o pixel da linha i, coluna j
    fim-para
fim-para

Relacionamentos entre pixels

Vizinhos de um pixel

Um pixel $p$ na coordenada $(x,y)$ tem quatro vizinhos horizontais e verticais, cujas coordenadas são dadas por:

$$(x+1,y), (x-1,y), (x,y+1), (x,y-1)$$

Esse conjunto de pixels, chamado de vizinhança-4 de $p$ é expresso por $N_4(p)$.

Os quatro vizinhos diagonais de $p$ têm coordenadas:

$$(x+1,y+1), (x+1,y-1), (x-1,y+1), (x-1,y-1)$$

que são expressas por $N_D(p)$. A união desses conjuntos forma a vizinhança-8 de p, expressa por $N_8(p)$.

Adjacência e conectividade, regiões e fronteiras

Expressamos por $V$ o conjunto de valores de intensidade utilizados para definir a adjacência. Há três tipos:

• adjacência-4: dois pixels $p$ e $q$ com valores pertencendo a $V$ são adjacentes se $q$ estiver no conjunto $N_4(p)$;
• adjacência-8: dois pixels $p$ e $q$ com valores pertencendo a $V$ são adjacentes-8 se $q$ estiver no conjunto $N_8(p)$;
• adjacência-m: dois pixels $p$ e $q$ com valores pertencendo a $V$ são adjacentes-m se: a) $q$ estiver em $N_q(p)$; ou b) $q$ estiver em $N_D(p)$ e o conjunto $N_4(p) \cap N_4(q)$ não contiver nenhum pixel cujos valores pertençam a $V$.

A figura a seguir ilustra esse conceito.

Um caminho (ou curva) do pixel $p$ com coordenadas $(x,y)$ para o pixel $q$ com coordenadas $(s, t)$ é uma sequência de pixels distintos com coordenadas:

$$(x_0,y_0),(x_1,y_1),...,(x_n,y_n)$$

onde $(x_0,y_0)=(x,y),(x_n,y_n)=(s,t)$ e os pixels $(x_i,y_i)$ e $(x_{i-1},y_{i-1})$ são adjacentes para $1 \leq i \leq n$. Nesse caso, $n$ é o comprimento do caminho. Se $(x_0,y_0)=(x_n,y_n)$, o caminho é fechado.

Com $S$ representando um subconjunto de pixels em uma imagem, dizemos que dois pixels $p$ e $q$ sao conexos em $S$ se houver um caminho entre eles consistindo inteiramente de pixels em $S$. Para qualquer pixel $p$ em $S$, o conjunto de pixels que são conectados a ele em $S$ é chamado de um componente conexo de $S$. Se existir apenas um componente conectado, o conjunto $S$ é chamado de conjunto conexo.

Com $R$ representando um subconjunto de pixels em uma imagem, chamamos de $R$ uma região da imagem se $R$ for um conjunto conexo. Duas regiões $R_1$ e $R_2$ são consideradas adjacentes se sua união formar um conjunto conexo. As regiões que não são adjacentes são disjuntas.

A fronteira (borda ou contorno) de uma região $R$ é o conjunto de pontos adjacentes aos pontos do complemento de $R$, ou seja, a fronteira de uma região é o conjunto de pixels da região que tem pelo menos um vizinho no fundo da imagem.

Medidas de distância

Para os pixels $p$, $q$ e $z$, com coordenadas $(x,y)$, $(s,t)$, $(v,w)$, respectivamente, $D$ é uma função distância ou medida de distância se:

a. $D(p,q) \geq 0$, com $D(p,q) = 0$ se $p = q$
b. $D(p,q) = D(q,p)$; e
c. $D(p,z) \leq D(p,q) + D(q,z)$.

A Distância Euclidiana entre $p$ e $q$ é definida como:

$$D_e(p,q) = ((x-s)^2 + (y-t)^2)^\frac{1}{2}$$

Para essa medida de distância, os pixels que possuem distância de $(x,y)$ menor ou igual a um valor $r$ são os pontos contidos em um disco de raio $r$ centrado em $(x,y)$.

Sugestão de leitura: Capítulos 1 e 2 de (GONZALEZ e WOODS, 2011)